原标题:如何优化均值方差模型?Min-Max最优化方法探索——金融工程专题报告来源:华宝财富魔方
分析师:张青(执业证书编号:S0890516100001)
研究助理:程秉哲
1952年,马科维兹提出了著名的均值方差模型,并以此开创了现代投资组合理论。该模型首次使用量化的方法,描述了投资组合中收益和风险的取舍,展示了分散投资的重要性。然而,均值方差模型的有效性很大程度上依赖于资产预期收益率和预期风险的准确度,这些指标在现实中又被公认是难以准确估计的。这就大大降低了均值方差模型的实践应用价值。为了缓解均值方差模型所生成的资产组合对预期收益和预期风险的敏感性,学者提出了多种鲁棒优化的方法来增加均值方差模型的实用性。
本期专题,我们提出了一套基于风险预算模型和Min-Max最优化模型的量化资产配置方法,并将其运用于股债配置中。该组合以债券资产配置为主(风险预算类模型决定了所生成的组合一定是以偏债为主的,因为债券资产的波动远小于股票资产,风险预算生成的初始配置权重会大幅倾向于债券资产配置),同时动态配置部分权益,可将其看做是一个固收+组合的具体运用。
为便于比较模型的优化结果,我们需要引入一个初始配置。我们考虑采用风险预算模型。风险预算模型的好处是仅基于资产的波动率生成组合权重,对输入并不敏感,且实际效果看,较之恒定权重配置,风险预算模型可以获取更优的收益风险比。
在用风险预算模型生成初始大类资产配置后,通过鲁棒优化后的均值方差模型来微调大类资产配置的权重以及中观行业配置优化。对于均值方差模型的鲁棒优化,我们主要参考Rustem, et al.(2000)提出的最小-最大(Min-Max)鲁棒最优化方法,通过输入多种收益/风险的情景来增加返回权重的健壮性。由于该方法的核心思想是针对市场最差可能发生情况的优化,我们认为其更加适合于风险厌恶场景下的投资组合构建。
本文结构安排如下:第一节介绍了风险预算模型在大类资产配置中的使用方法;第二节介绍了传统均值方差问题的构建并展示回测结果;第三节介绍了Rustem, et al.(2000)的Min-Max最优化方法,并展示了基于该方法优化后的均值方差模型回测结果;第四节在Min-Max优化中纳入中观行业的遴选并展示回测结果;第五节尝试使用自助抽样(bootstrap)的方法缓解均值方差模型生成权重值稀疏的问题。
1. 基于风险预算模型的大类资产权重生成
1.1. 风险预算模型介绍
由于其在平滑收益曲线上的优异表现,风险预算模型被广泛应用在大类资产配置上。相比均值方差模型,风险预算模型不需要使用者输入难以准确预测的预期收益率,唯一的输入参数是所有资产的协方差矩阵,这大大提升了风险预算模型的样本外效果。顾名思义,风险预算模型要求各类资产的风险贡献满足一个指定的比例,风险平价模型就是风险预算模型的风险贡献为等权时的特例。一般来说,风险预算模型的权重生成过程如下:
对于权重向量为w,由m个资产组成的资产组合,若各资产的协方差矩阵为Σ,那么该组合的风险即为:
资产i的边际风险(MR):

资产i的总风险(TR):
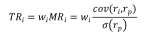
若资产i和资产j的配置比例设置为bi和bj,那么在风险预算模型的设定中,资产i和资产j的总风险需要满足下列等式:
当资产多于2个时,难以直接通过上面等式形成的方程组直接求出权重向量w的解,因此在实际应用中,通常通过建立一个优化问题的方式来找到最优权重:
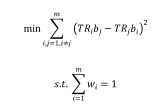
本期专题中,我们主要是使用权益和固收类资产来合成固收加组合,因此大类资产配置中只涉及到股债两类资产。在这种情况下,可以对上述的求解过程做进一步的简化。资产组合的风险可以写成:
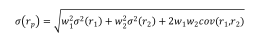
资产1边际风险即对上式关于w1求导,
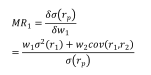
资产1总风险贡献:
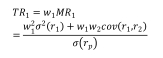
同理,资产2总风险贡献:
那么就有:
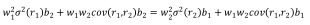
此时,如果资产1和资产2的风险预算相同(也就是风险平价模型的情况),很容易可以看出两个资产权重之比即为波动率的倒数之比。若风险预算不是1:1,那么可以通过权重相加等于1的条件,将上式转化成一个关于w1或者w2的二元一次方程,也可轻松求解。
1.2. 基于风险预算模型的大类资产配置回测结果
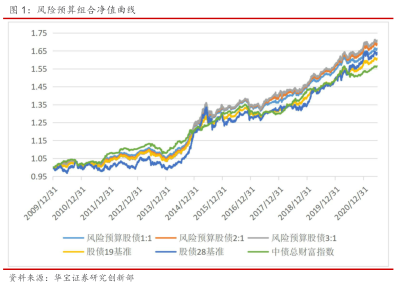
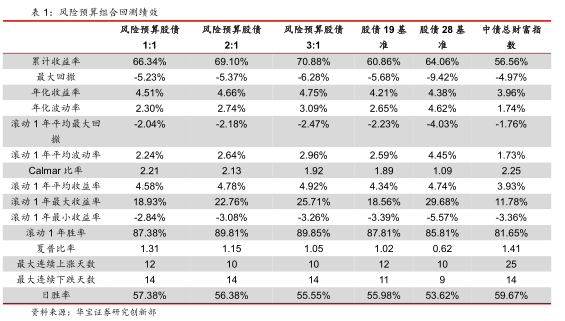
我们用沪深300指数(000300.SH)代表权益资产,中债总财富指数(CBA00301.CS)代表债券资产。回测了不同的风险预算下组合的净值表现。我们分别尝试了股债风险配置1:1、2:1和3:1三种情况,并和股债1:9,2:8配置的基准做对比。
回测时间区间为2010年1月4日-2021年6月30日,调仓日(对于基准就是再平衡日)为每季度第一个交易日。在每个调仓日,用最近1年的数据计算协方差矩阵,测试结果如下。
从回测结果上来看,相交于基准,风险预算模型确实显著提升了组合的收益风险特征。风险预算股债1:1组合的平均权益仓位不足10%,但其年化收益率比股债19和28的基准都更高,回撤指标也显著小于两个基准。风险预算股债2:1组合和风险预算股债3:1组合也都用更小的仓位达到了比股债28基准组合更高的收益率和更优的收益风险比。
在三个风险预算组合中,风险预算1:1的组合收益风险比最优,其年化收益率较最为激进的风险预算1:3组合也只少了0.24%,但最大回撤提升1.05%。因此在后续均值方差模型的研究中,我们使用风险预算1:1组合作为基准,在此基础上做进一步的优化。从固收加的角度上来讲,该组合相较中债总财富指数的年化收益率增厚0.55%,并且最大回撤只多了0.26%。
2. 传统均值方差模型
在介绍Min-Max最优化模型之前,我们先测试传统均值方差模型的表现。这样一是可以描述我们对基础优化问题的构建方式,二是可以作为Min-Max最优化模型的比较基准。
2.1. 最优化问题的构建
一般来说,均值方差模型最优化问题可分为三类:第一类是给定一个最小收益,使得风险最小化;第二类是给定一个最大波动率,试图去最大化组合收益;第三类是最优化效用函数,通常需要指定一个风险厌恶系数。第一类优化问题最为常见,但是若最小收益的限制设置的不恰当、或者各资产的预期收益过小,就会很容易造成优化问题无可行解。对于第二类优化问题来说,一是也有可能因为对波动率的设置过于严格而导致无可行解,二是波动率不如收益率来的直观,很难对其设置一个合理的限制条件。因此我们选择使用第三类优化问题,即效用函数的优化。
效用最优化问题的构建如下:
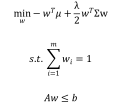
可以看到,虽然效用优化问题不需要设置最小收益或最大波动率的限制条件,但是在目标函数中仍然有一个风险厌恶系数lambda需要设定。该数值越大,说明风险在效用函数中的占比越大,投资者也更加的风险厌恶。对于风险厌恶系数的设定,实践中通常取2-4中的一个数,因此我们设其为3。在限制条件中,除了基本的权重和为1之外,还有一些不等式条件。假设风险预算模型所生成的大类资产权重为1-a%和a%(分别是债和股的权重),我们允许权益仓位的有上下50%的浮动,也就是a/2%到3a/2%之间。那么债券基金仓位的范围就是1-3a/2%到1-a/2%。
2.2. 回测表现
回测时间区间为2010年1月4日-2021年6月30日,调仓日为每季度第一个交易日。在每个调仓日,用最近1年的数据计算预期收益率和协方差矩阵。
从回测结果上来看,均值方差组合的表现并没能够在风险平价组合上有进一步的提升,不仅在收益上弱于风险平价组合,并且回撤也比风险平价组合更大。均值方差组合的卡玛比率只有1.75,大幅低于风险平价组合的2.21。均值方差模型样本外的不稳定性,以及对预期收益和协方差矩阵的依赖性成为了其被业界广泛使用的阻碍。
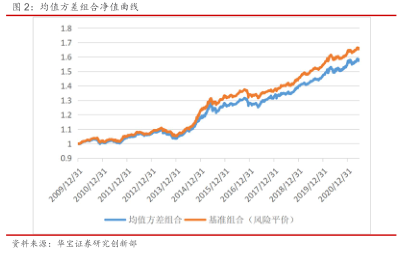
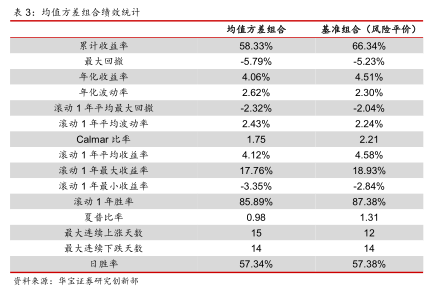
3. Min-Max最优化模型
3.1. Min-Max最优化框架介绍
Min-Max最优化法是对传统马科维兹框架的拓展,最早由Rustem, et al.(2000)提出。为了缓解预期收益和预期风险的不准确性,在Min-Max最优化的框架下,投资者可以假定多种不同的收益风险场景,并将这些不同场景下的收益风险组合作为参数一并输入。Min-Max最优化模型则试图输出一个最优化最差场景的权重。
考虑以下传统均值方差优化模型,其中J(w)是我们想要进行优化的目标函数,W是w的限定条件。
在Min-Max最优化的框架下,我们引入多个目标函数(n个场景):
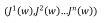
最优化问题即为:
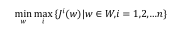
在这个优化问题里,里层的max即代表所有场景中的最差情况,外层的min就是对这个最差情况的最优化。对该最优化问题的一个比较直观的理解是:对于每一个可行的权重向量w,依次将其带入n个目标函数中,并得到所有目标函数的最大值(即最坏情况)。这样每一个w就对应一个最大值。然后在这些w中,所对应最大值最小的那个w就是Min-Max最优化中的最优解。
在实际求解中,w的可行范围通常是一个连续的空间,无法通过穷举的方法来求解。Rustem, et al.(2000)指出,若w的限制条件皆为线性等式和不等式,那么该优化问题的求解会容易很多,在Rustem, et al.(2000)的第三部分,作者给出了针对线性限制条件的求解算法。由于本报告并未直接应用上述的Min-Max最优化框架,而是采用了一个变种,因此在本报告中就不对求解算法做详细的介绍。
Min-Max最优化问题可以视为对所有场景可能出现的最差情况的保护,很显然这仅限于输入进模型中的n个场景,但对于未输入模型中的场景,Min-Max最优化问题也可能提供一定程度的保护。
设一个向量k满足以下条件:
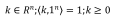
并定义一个元素为n个场景的向量:
那么Min-Max最优化问题可以等价替换为下述最优化问题:
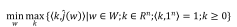
在对于向量k的限制条件下,k和情景向量的点乘即所有情景的凸组合。也就是说,Min-Max最优化问题对输入场景所合成的凸组合也有保护的效果。
有些时候,最差情况太过极端会导致组合过于保守。因此Rustem, et al.(2000)提出,可以让投资者预先设置向量k,该向量代表投资者对各个情景发生可能性的判断,这样,上述Min-Max最优化问题就可以得到进一步简化:
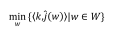
鉴于其灵活度较高,而且更契合投资者的直观,本报告中我们采用该简化后的Min-Max最优化框架。
3.2. 情景的构建和权重的生成
对于情景的构建,Rustem, et al.(2000)提供了四种可能的方式
1. 不同的预期收益,相同的预期风险
2. 不同的预期收益,不同的预期风险
3. 不同的预期收益-预期风险组合
4. 相同的预期收益,不同的预期风险
首先,预期收益作为一个重要变量,在不同的场景中是要有所区分的,因此排除方式4。在方式1、2、3中,由于我们的场景是直接从历史数据中提取的,因此方式3使用起来最为直观和方便。
我们用沪深300的市净率分位数来划分三个不同的场景。具体来说,在某一个调仓日,对于过去5年的每一个交易日,统计未来三个月的收益向量和协方差矩阵。再通过过去五年沪深300市净率的排名情况,将过去五年的交易日分为估值极端高、估值极端底、和估值中等三个场景。最后,将这三个场景中的收益向量和协方差矩阵求平均值,即可得到三个情景下的预期收益-预期风险组合。
对于这三种场景的权重,我们以当前调仓日的市净率所处过去5年分位数作为参考。当前市净率分位数越高,就给高估值场景分配更多的权重。具体来说,我们给高估值、中估值、低估值三个场景都设置了一个平均估值分位数,分别是95%,50%,5%。如果当前估值分位数是90%,那么三个场景的权重之比即当前估值和三个平均估值的距离的倒数:
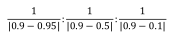
在此基础上,为了体现固收加类产品对于风险的厌恶,我们将当前的估值分位数适当的提高,这样可以使得高估值场景获得更高的权重。
3.3. 回测表现
回测设置和3.2中的一致。从回测结果上来看,虽说Min-Max最优化组合的收益率仍然略低于均值方差组合,但最大回撤比均值方差组合缩小了0.14%,滚动一年最大回撤更是从2.04%大幅下降到1.54%。收益风险比上,Min-Max最优化组合的卡玛比率和夏普比率皆要优于均值方差组合。回测结果证实了Min-Max最优化方法的有效性。
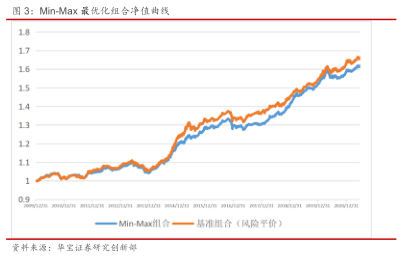
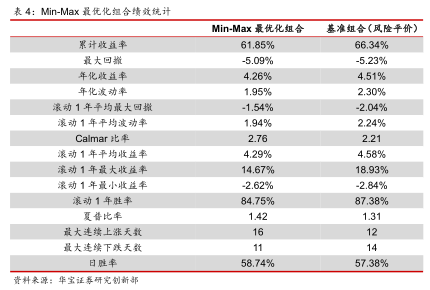
4. Min-Max最优化在中观配置上的检验
在前文中,我们已经展示了Min-Max最优化在大类资产配置中的有效性。但在只有股债两类资产的情况下,给Min-Max最优化的提升空间较小,因此我们将其应用拓展至中观层面,倘若我们在权益配置上增加更多的选择,或许能进一步提升Min-Max最优化的效果。
4.1. 权益资产遴选
均值方差优化模型对输入极为敏感,要达到更好的风险分散效果、提升模型的样本外表现,我们希望所选入的资产之间差异要尽量大,也就是说相关性要足够低。另一方面,我们希望所选基金的风格是相对稳定的,这样才能让历史的净值走势特征更有延续性,而一般的主动权益基金并不能满足这一要求。综合考虑,我们决定使用行业ETF基金作为底层权益资产。我们先统计所有28个申万一级行业指数之间的相关性,再通过对相关系数系数矩阵聚类的手段,筛选出相互之间相关性较小的行业,最后还需要确保所选行业都有可投基金标的。
统计过去11年的数据,各行业之间的相关性系数如下图所示:
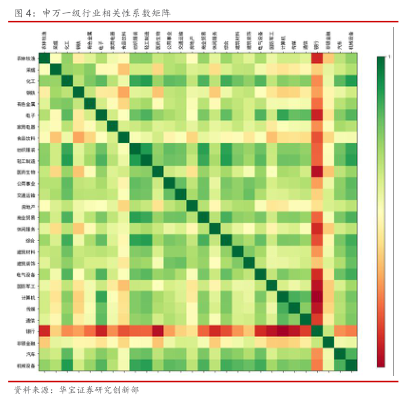
我们通过层次聚类的方法,把上面相关性矩阵的行列重新排列,将相似的行业聚集在一起:
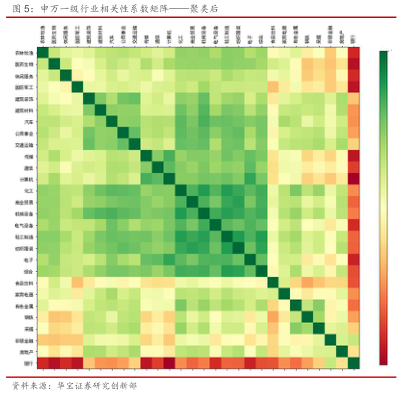
可明显看到,有一些高相关性的行业被聚集在了一起,形成一个大类(沿着对角线的深绿色方形区间)。对于处于同一类的行业,我们只需要选出一个行业作为代表即可。这样可以达到降低底层资产之间整体相关性的效果。
最后我们检查所选行业是否有对应的基金标的,最终的入选行业和具体基金标的如下。由于很多基金的成立时间不够长,在后续的回测中我们仍然使用相对应的申万一级行业指数作为底层资产。
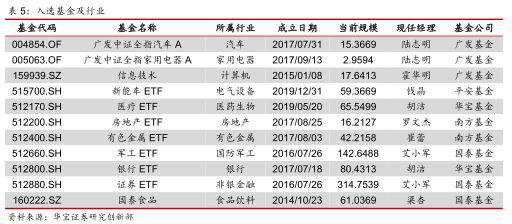
4.2. 均值方差模型
在优化问题的建立和大类资产的权重限制上,我们沿用了2.1中的设定。对于单个权益资产的上下界设置,我们限制仓位在0%-a/2%之间(a为风险平价模型所生成的大类资产权益仓位)。
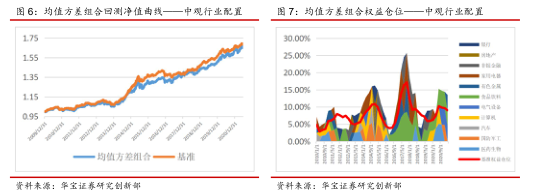
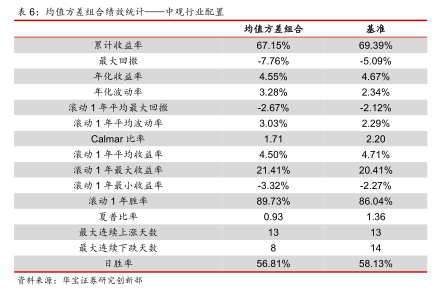
图4展示了基于传统均值方差模型的回测结果,并和基准相比较。该基准组合在大类资产配置上采用风险平价模型生成,并在权益资产的细分资产上采用等权配置。从回测结果上来看,经过均值方差模型优化的组合的表现显著弱于基准组合。均值方差优化组合的年化收益率为4.55%,小于基准组合0.12%,但最大回撤达到了-7.76%,比基准组合多出了2.67%。究其原因,我们可以从图5的权益资产仓位中找到一些线索。在15年4月初的调仓日,由于权益市场在过去一年表现良好,均值方差模型组合相比基准配置了更多的权益,这也导致组合在15年的大跌中承受了更大的回撤。
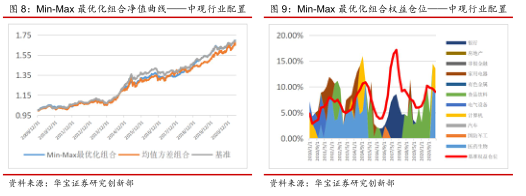
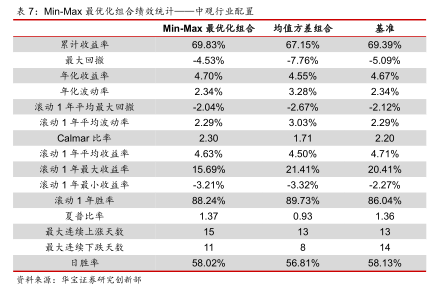
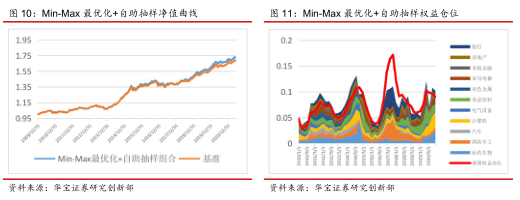
4.3. Min-Max最优化
我们沿用4.2中的回测设置和基准,Min-Max最优化法的回测表现如下。在收益基本维持不变的情况下,Min-Max最优化组合的最大回撤仅为-4.53%,相较基准缩小了0.56%。在以pb分位数划分情景的框架下,15年之后的权益仓位都是偏谨慎的,但收益仍然不输传统均值方差优化组合。可以看到,在加入了中观标的后,Min-Max最优化模型也有不错的表现。
5. 自助抽样法
不管是传统均值方差模型,还是Min-Max最优化模型,每期的权重都只集中在少数的资产上,这从一定程度上也会加大组合对单个行业暴露的风险,违背了构建投资组合的初衷。我们利用自助抽样法,基于不同的样本生成多个最优权重向量,再将对这些权重求平均值即可得到抽样后的最优权重。假设有A,B,C三个资产,总共进行两次抽样,第一次抽样所得到的权重分别为0.5、0.5、0,第二次抽样所得到的权重分别为0、0.5、0.5,那么抽样后的平均权重即为0.25,0.5,0.25。在两次单独的抽样中,分别只有两个资产被分配了权重,但抽样后的权重在三个资产上都有配置,权重更加分散。
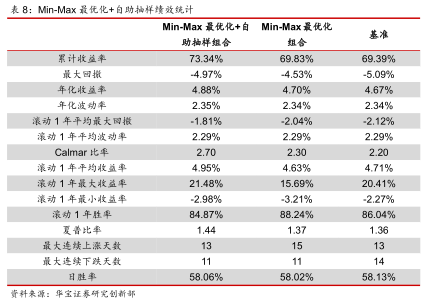
我们在Min-Max最优化的基础上叠加自助抽样法。我们使用一种非参数的自助抽样方法,对高估值、中估值和低估值三种场景分别生成100个样本。对于某个场景的单个样本的生成,随机选取过去五年估值分位数在该场景范围区间的某一个交易日,统计未来一个季度的收益率和协方差矩阵。Min-Max最优化叠加自助抽样的回测结果如下。
可以看到,叠加自助抽样法后,组合收益有了进一步提升,年化收益率达到4.88%,高于基准组合的4.67%。虽然最大回撤较单纯的Min-Max最优化组合有所增加,但是仍然小于基准组合。叠加了自助抽样法的Min-Max最优化组合在卡玛比率、夏普比率和滚动一年最大回撤上皆较叠加前有显著的提升。
6. 总结
本期专题,我们基于Min-Max最优化和自助抽样法对传统均值方差模型做了改进,并且结合风险预算模型以构建具有良好收益风险比的固收加基金组合。我们的实证研究表明Min-Max最优化的框架能在一定程度上改善传统均值方差模型样本外表现的不稳定。但正如Rustem, et al.(2000)的作者所说,不能简单的把Min-Max最优化作为均值方差模型输入的替代,其有效性很大程度上还是取决于对场景的准确选择。因此,本报告的价值更多在于提供一种基金组合的构建框架。对于具体的场景选择,除了本报告提出的用宽基指数市净率分位数分档外,也有非常大的拓展空间。

郑重声明:本文版权归原作者所有,转载文章仅为传播更多信息之目的,如作者信息标记有误,请第一时间联系我们修改或删除,多谢。



